We have a wide offering of general education courses designed to prepare you to major in Business and STEM (Science, Technology, Engineering, and Mathematics) fields.
Student Focused
In Active Grants
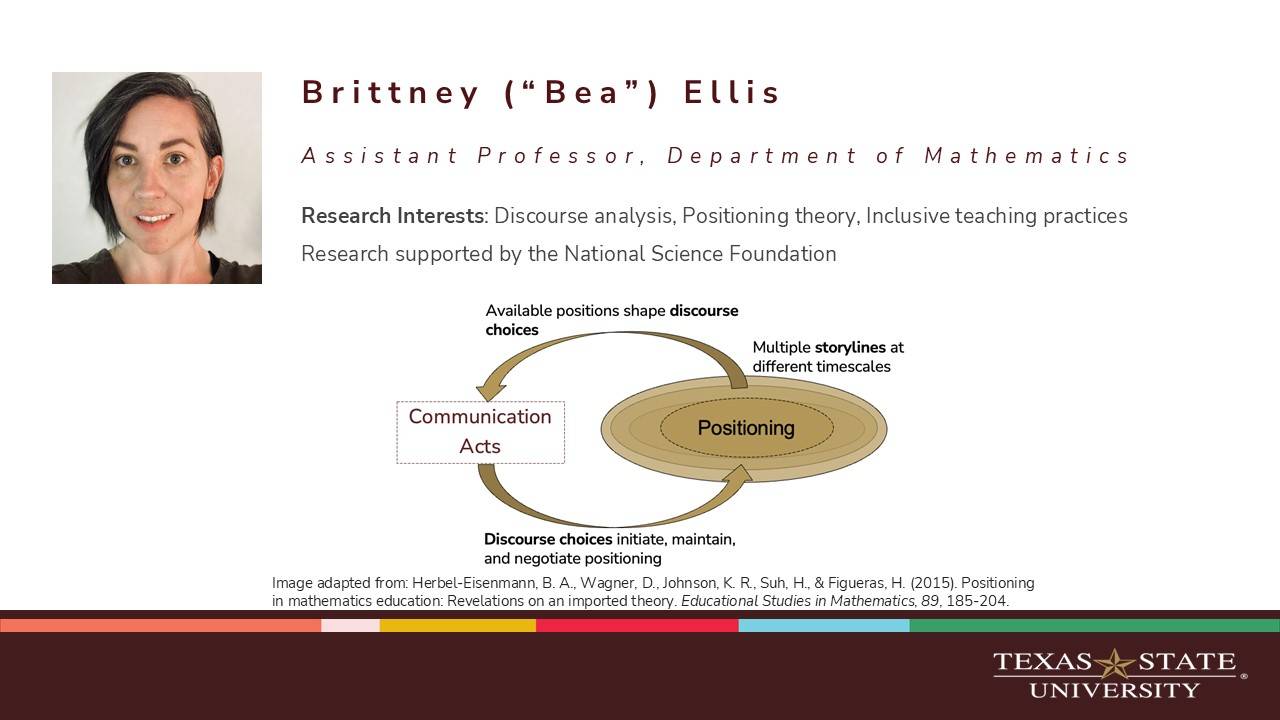
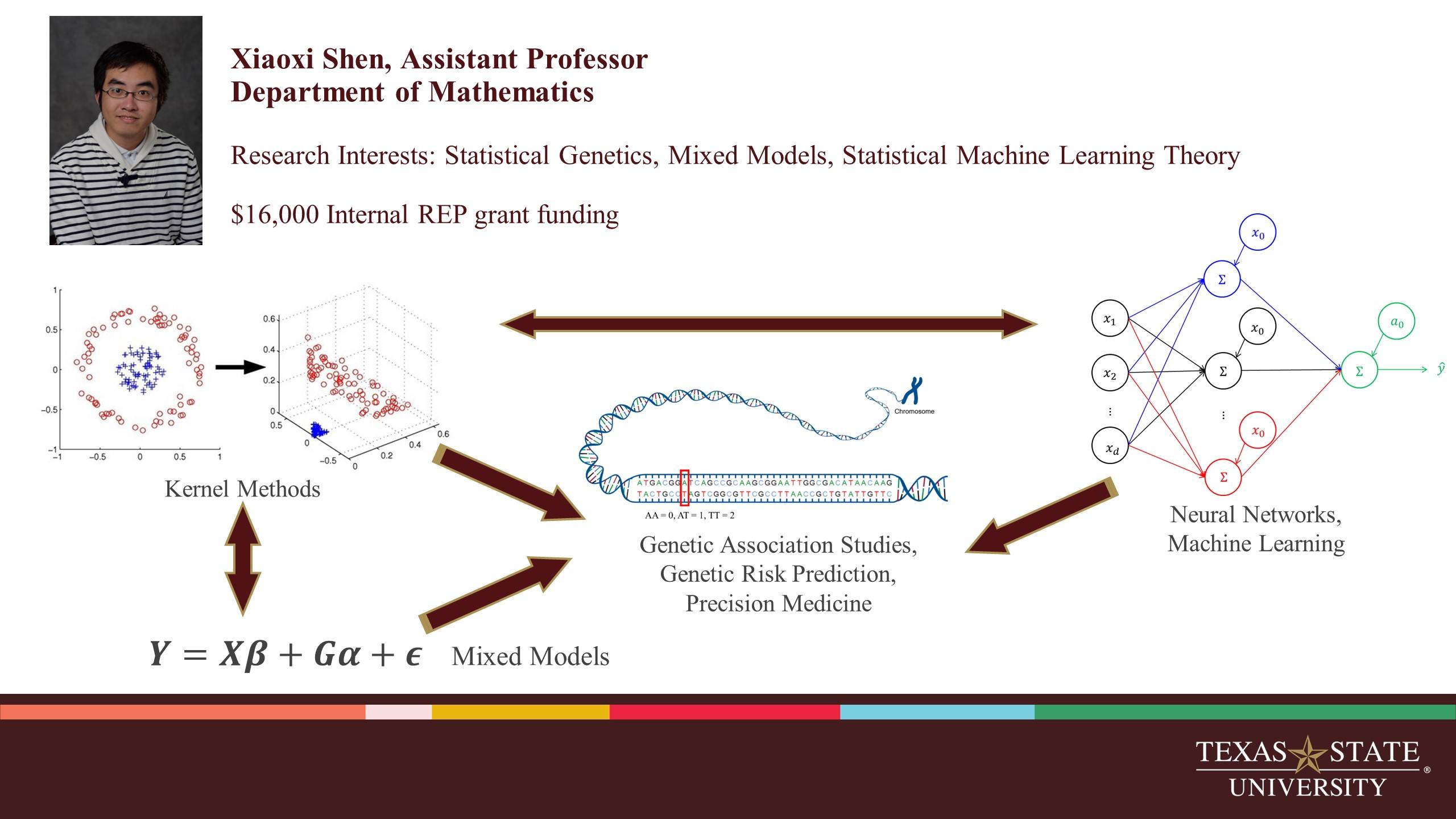
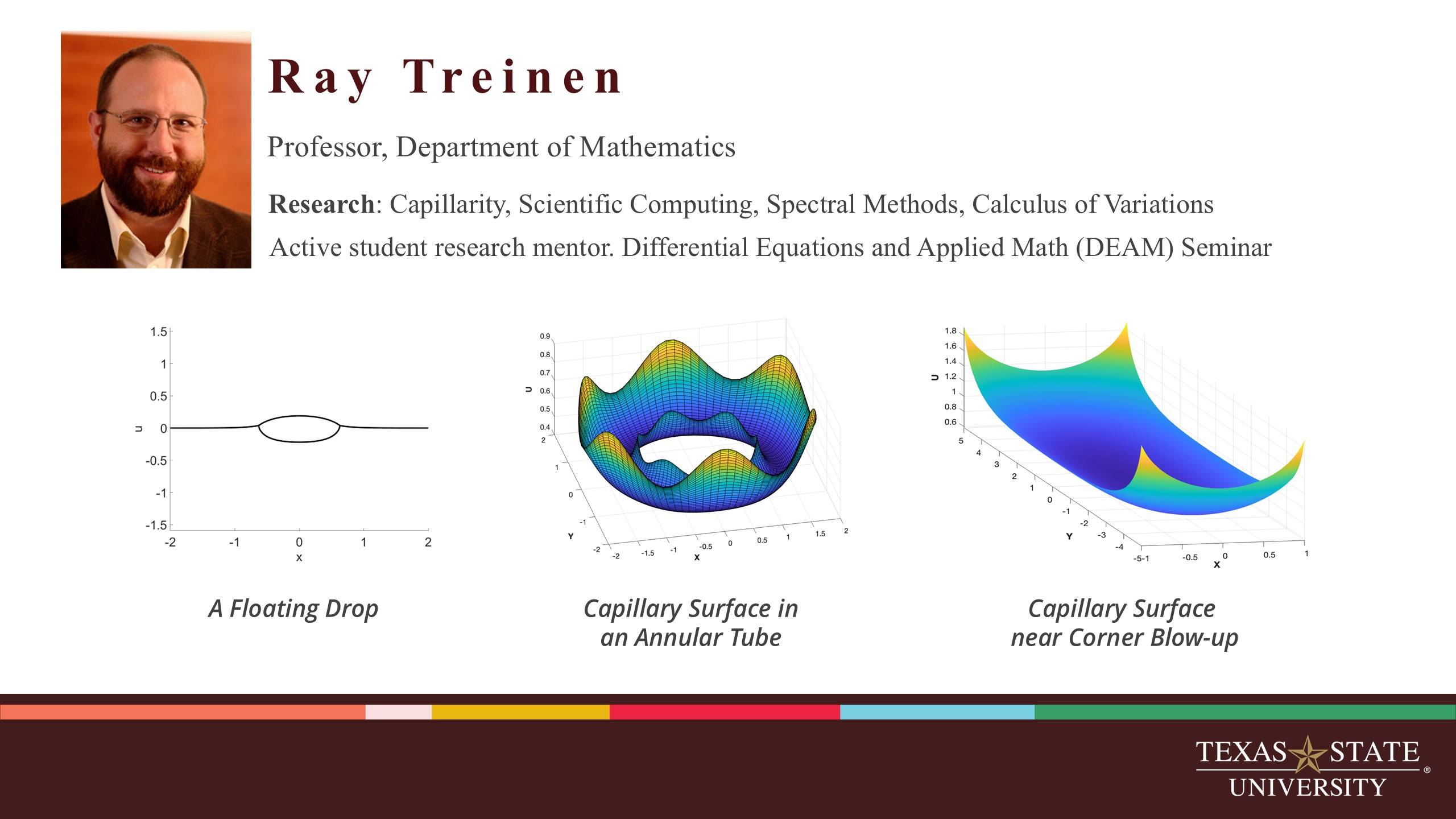
Discover our dynamic faculty and the innovative research they’re driving through, high-impact grant awards.
NEXT in Math
Promotion from Assistant Professor to Associate Professor & Tenure
Hiroaki Tanaka
Promotion from Associate Professor to Professor
Kathleen Melhuish and Hiroko Warshauer
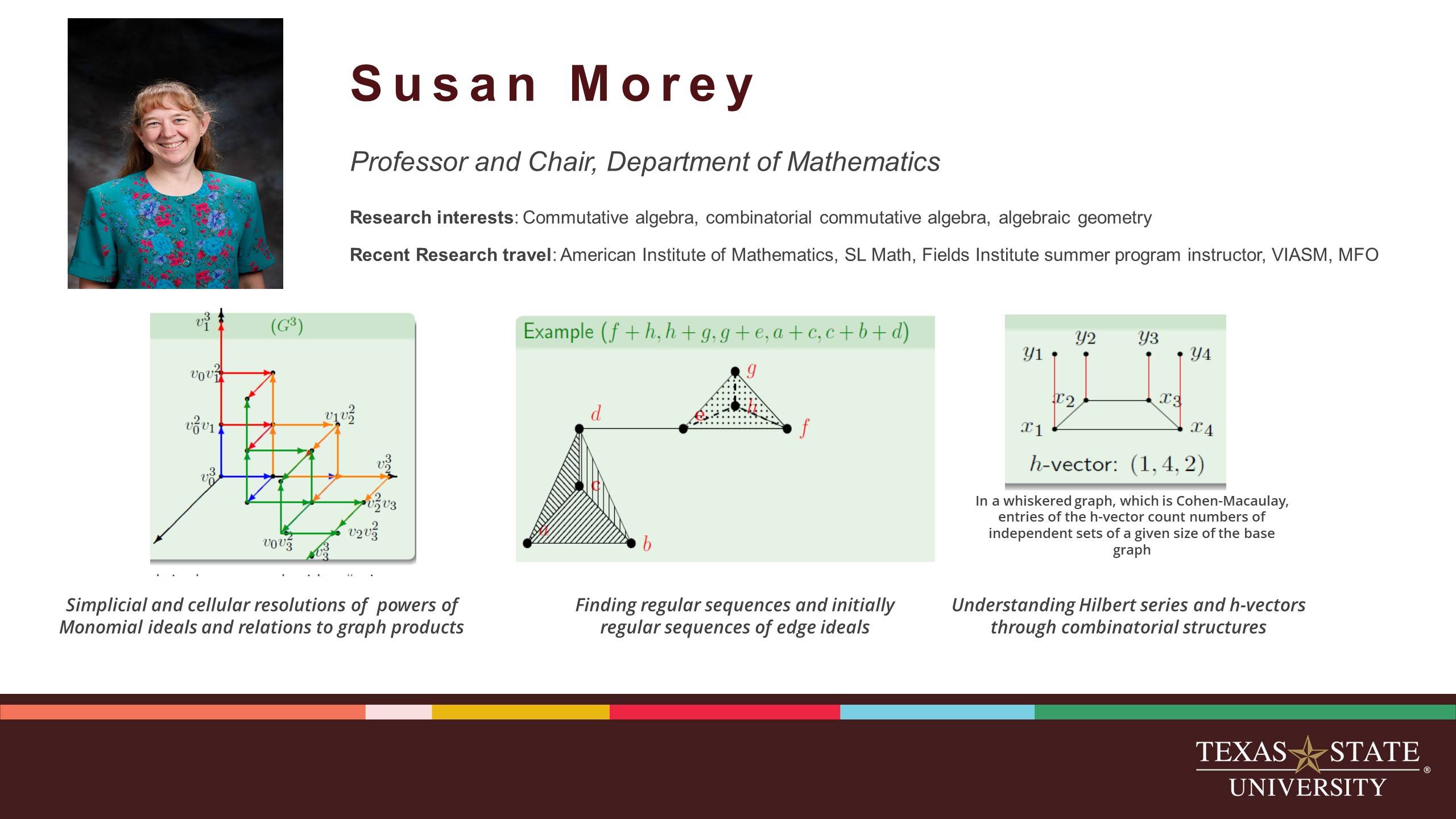
Dr. Susan Morey Receives the University Distinguished Professor Award
This award honors individuals whose performance in teaching, research, and service has been exemplary and recognized at the state, national, and international levels.
@TXST Math
- Location:
- DERR 121; 121
- Cost:
- Free
- Contact:
- Anton Dochtermann
dochtermann@txstate.edu
This seminar meets about once a week. The format is very informal, the idea is that we collectively select a topic for the semester and present material surround that theme. Original research is not typically presented and we encourage participation from all levels. Graduate students with an interest in algebra/combinatorics are especially encouraged to attend.
Click here for more information
more about event
- Location:
- DERR 120; 120
- Cost:
- Free
- Contact:
- Cameron Farnsworth
clf129@txstate.edu - Campus Sponsor:
- Department of Mathematics
Love a good problem? Like to solve difficult puzzles?
Join professors, graduate students and undergraduates as we tackle problems presented from several mathematical journals. An interest in higher level mathematics is all that is required to join our round table. Offer what you know, learn what you don't in a relaxed environment with some of our department's finest!
Join professors, graduate students and undergraduates as we tackle problems presented from several mathematical journals. An interest in higher level mathematics is all that is required to join our round table. Offer what you know, learn what you don't in a relaxed environment with some of our department's finest!
- Location:
- DERR 325; 325
- Cost:
- Free
- Contact:
- Christine R.S. Lee
vne11@txstate.edu - Campus Sponsor:
- Department of Mathematics
Birch Bryant from the University of North Alabama will tells us about “Hidden obstructions to efficient triangulated Dehn fillings.”
Click here for more information
more about event
- Location:
- Zoom only
- Cost:
- Free
- Contact:
- Vera Ioudina
vi11@txstate.edu - Campus Sponsor:
- Department of Mathematics
Kevin Slote
Georgia State University
Causal Network discovery with the open-source Causation Entropy software library Click here for more information
more about event
Georgia State University
Causal Network discovery with the open-source Causation Entropy software library Click here for more information
- Location:
- DERR 325; 325
- Cost:
- Free
- Contact:
- Ray Treinen
treinen@txstate.edu - Campus Sponsor:
- Department of Mathematics
- Location:
- DERR 120; 120
- Cost:
- Free
- Contact:
- Christine R.S. Lee
vne11@txstate.edu - Campus Sponsor:
- Department of Mathematics
Dr. Jeremiah Birrell (Texas State University) will give us an introduction to "Concentration Inequalities and the Entropy Method” .
Click here for more information
more about event
- Location:
- DERR 121; 121
- Cost:
- Free
- Contact:
- Anton Dochtermann
dochtermann@txstate.edu
This seminar meets about once a week. The format is very informal, the idea is that we collectively select a topic for the semester and present material surround that theme. Original research is not typically presented and we encourage participation from all levels. Graduate students with an interest in algebra/combinatorics are especially encouraged to attend.
Click here for more information
more about event